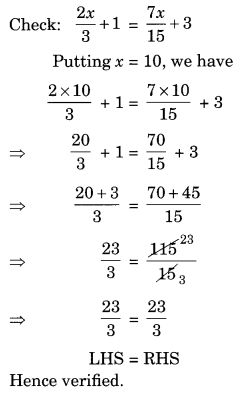Class-8 Subject- MATHS CHAPTER-2(EXERCISE 2.2 & 2.3) LINEAR EQUATIONS IN ONE VARIABLE

EVENTS CONVENT HIGH SCHOOL
24/08/2021          CLASS-8         SESSION2021-22(SLOT-1)
Maths
Chapter-2
LINEAR EQUATIONS IN ONE VARIABLE 
______________________________________

EXERCISE 2.2

Question 4.Sum of two numbers be 95. If one exceeds the other by 15, find the numbers.
Solution:
Let one number be x
Other number = x + 15
As per the condition of the question, we get
x + (x + 15) = 95
⇒ x + x + 15 = 95
⇒ 2x + 15 = 95
⇒ 2x = 95 – 15 [transposing 15 from (+) to (-)]
⇒ 2x = 80
⇒ x = 802 [transposing 2 from (×) to (÷)]
⇒ x = 40
Other number = 95 – 40 = 55
Thus, the required numbers are 40 and 55.

Question 5.Two numbers are in the ratio 5 : 3. If they differ by 18, what are the numbers?
Solution:
Let the two numbers be 5x and 3x.
As per the conditions, we get
5x – 3x = 18
⇒ 2x = 18
⇒ x = 18 ÷ 2 [Transposing 2 from (×) to (÷)]
⇒ x = 9.
Thus, the required numbers are 5 × 9 = 45 and 3 × 9 = 27

Question 6.Three consecutive integers add up to 51. What are these integers?
Solution:
Let the three consecutive integers be x, x + 1 and x + 2.
As per the condition, we get
x + (x + 1) + (x + 2) = 51
⇒ x + x + 1 + x + 2 = 51
⇒ 3x + 3 = 51
⇒ 3x = 51 – 3 [transposing 3 to RHS]
⇒ 3x = 48
⇒ x = 48 ÷ 3 [transposing 3 to RHS]
⇒ x = 16
Thus, the required integers are 16, 16 + 1 = 17 and 16 + 2 = 18, i.e., 16, 17 and 18.

EXERCISE 2.3

Question 1.3x = 2x + 18

Solution:
We have 3x = 2x + 18
⇒ 3x – 2x = 18 (Transposing 2x to LHS)
⇒ x = 18
Hence, x = 18 is the required solution.
Check: 3x = 2x + 18
Putting x = 18, we have
LHS = 3 × 18 = 54
RHS = 2 × 18 + 18 = 36 + 18 = 54
LHS = RHS
Hence verified.

 Question 2.5t – 3 = 3t – 5
Solution:
We have 5t – 3 = 3t – 5
⇒ 5t – 3t – 3 = -5 (Transposing 3t to LHS)
⇒ 2t = -5 + 3 (Transposing -3 to RHS)
⇒ 2t = -2
⇒ t = -2 ÷ 2
⇒ t = -1
Hence t = -1 is the required solution.
Check: 5t – 3 = 3t – 5
Putting t = -1, we have
LHS = 5t – 3 = 5 × (-1)-3 = -5 – 3 = -8
RHS = 3t – 5 = 3 × (-1) – 5 = -3 – 5 = -8
LHS = RHS
Hence verified.

Question 3.5x + 9 = 5 + 3x
Solution:
We have 5x + 9 = 5 + 3x
⇒ 5x – 3x + 9 = 5 (Transposing 3x to LHS) => 2x + 9 = 5
⇒ 2x = 5 – 9 (Transposing 9 to RHS)
⇒ 2x = -4
⇒ x = -4 ÷ 2 = -2
Hence x = -2 is the required solution.
Check: 5x + 9 = 5 + 3x
Putting x = -2, we have
LHS = 5 × (-2) + 9 = -10 + 9 = -1
RHS = 5 + 3 × (-2) = 5 – 6 = -1
LHS = RHS
Hence verified.

Question 4.4z + 3 = 6 + 2z
Solution:
We have 4z + 3 = 6 + 2z
⇒ 4z – 2z + 3 = 6 (Transposing 2z to LHS)
⇒ 2z + 3 = 6
⇒ 2z = 6 – 3 (Transposing 3 to RHS)
⇒ 2z = 3
⇒ z = 32
Hence z = 32 is the required solution.
Check: 4z + 3 = 6 + 2z
Putting z = 32, we have
LHS = 4z + 3 = 4 × 32 + 3 = 6 + 3 = 9
RHS = 6 + 2z = 6 + 2 × 32 = 6 + 3 = 9
LHS = RHS
Hence verified.

Question 5. 2x – 1 = 14 – x
Solution:
We have 2x – 1 = 14 – x
⇒ 2x + x = 14 + 1 (Transposing x to LHS and 1 to RHS)
⇒ 3x = 15
⇒ x = 15 ÷ 3 = 5
Hence x = 5 is the required solution.
Check: 2x – 1 = 14 – x
Putting x = 5
LHS we have 2x – 1 = 2 × 5 – 1 = 10 – 1 = 9
RHS = 14 – x = 14 – 5 = 9
LHS = RHS
Hence verified.

Question 6.8x + 4 = 3(x – 1) + 7
Solution:
We have 8x + 4 = 3(x – 1) + 7
⇒ 8x + 4 = 3x – 3 + 7 (Solving the bracket)
⇒ 8x + 4 = 3x + 4
⇒ 8x – 3x = 4 – 4 [Transposing 3x to LHS and 4 to RHS]
⇒ 5x = 0
⇒ x = 0 ÷ 5 [Transposing 5 to RHS]
or x = 0
Thus x = 0 is the required solution.
Check: 8x + 4 = 3(x – 1) + 7
Putting x = 0, we have
8 × 0 + 4 = 3(0 – 1) + 7
⇒ 0 + 4 = -3 + 7
⇒ 4 = 4
LHS = RHS
Hence verified.

 Question 7 x = 45 (x + 10)
Solution:
We have x = 45 (x + 10)
⇒ 5 × x = 4(x + 10) (Transposing 5 to LHS)
⇒ 5x = 4x + 40 (Solving the bracket)
⇒ 5x – 4x = 40 (Transposing 4x to LHS)
⇒ x = 40
Thus x = 40 is the required solution.
Check: x = 45 (x + 10)
Putting x = 40, we have
40 = 45 (40 + 10)
⇒ 40 = 45 × 50
⇒ 40 = 4 × 10
⇒ 40 = 40
LHS = RHS
Hence verified.

Question 8. 2x3 + 1 = 7x15 + 3
Solution:
We have 2x3 + 1 = 7x15 + 3
15(2x3 + 1) = 15(7x15 + 3)
LCM of 3 and 15 is 15
2x3 × 15 + 1 × 15 = 7x15 × 15 + 3 × 15 [Multiplying both sides by 15]
⇒ 2x × 5 + 15 = 7x + 45
⇒ 10x + 15 = 7x + 45
⇒ 10x – 7x = 45 – 15 (Transposing 7x to LHS and 15 to RHS)
⇒ 3x = 30
⇒ x = 30 ÷ 3 = 10 (Transposing 3 to RHS)
Thus the required solution is x = 10