CLASS-9 SUBJECT MATHS (FINALS-E) CHAPTER-7 (EXERCISE 7.4) TRIANGLES.

 EVENTS CONVENT HIGH SCHOOL

27/01/2022      CLASS- 9   SESSION 2021-22
SUBJECT : MATHS

CHAPTER-7 (EXERCISE7.4)
TRIANGLES

______________________________________

Question 1.Show that in a right angled triangle, the hypotenuse is the longest side.
Solution:
Let us consider ∆ABC such that ∠B = 90°
∴ ∠A + ∠B + ∠C = 180°
⇒ ∠A + 90°-+ ∠C = 180°
⇒ ∠A + ∠C = 90°
⇒∠A + ∠C = ∠B
∴ ∠B > ∠A and ∠B > ∠C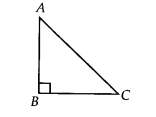

⇒ Side opposite to ∠B is longer than the side opposite to ∠A
i.e., AC > BC.
Similarly, AC > AB.
Therefore, we get AC is the longest side. But AC is the hypotenuse of the triangle. Thus, the hypotenuse is the longest side.

Question 2.In figure, sides AB and AC of ∆ABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.

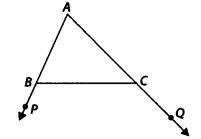
Solution:
∠ABC + ∠PBC = 180° [Linear pair]
and ∠ACB + ∠QCB = 180° [Linear pair]
But ∠PBC < ∠QCB [Given] ⇒ 180° – ∠PBC > 180° – ∠QCB
⇒ ∠ABC > ∠ACB
The side opposite to ∠ABC > the side opposite to ∠ACB
⇒ AC > AB.

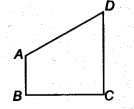
Question 3.In figure, ∠B <∠ A and ∠C <∠ D. Show that AD < BC.

Solution: Since ∠A > ∠B [Given]
∴ OB > OA …(1)
[Side opposite to greater angle is longer]
Similarly, OC > OD …(2)
Adding (1) and (2), we have
OB + OC > OA + OD
⇒ BC > AD

Question 4.AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see figure). Show that ∠ A > ∠C and ∠B >∠D.

Solution:
Let us join AC.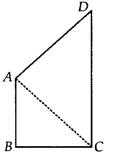

Now, in ∆ABC, AB < BC [∵ AB is the smallest side of the quadrilateral ABCD] ⇒ BC > AB
⇒ ∠BAC > ∠BCA …(1)
[Angle opposite to longer side of A is greater]
Again, in ∆ACD, CD > AD
[ CD is the longest side of the quadrilateral ABCD]
⇒ ∠CAD > ∠ACD …(2)
[Angle opposite to longer side of ∆ is greater]
Adding (1) and (2), we get
∠BAC + ∠CAD > ∠BCA + ∠ACD
⇒ ∠A > ∠C
Similarly, by joining BD, we have ∠B > ∠D.

Question 5.In figure, PR > PQ and PS bisect ∠QPR. Prove that ∠PSR >∠PSQ.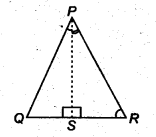

Solution:
In ∆PQR, PS bisects ∠QPR [Given]
∴ ∠QPS = ∠RPS
and PR > PQ [Given]
⇒ ∠PQS > ∠PRS [Angle opposite to longer side of A is greater]
⇒ ∠PQS + ∠QPS > ∠PRS + ∠RPS …(1) [∵∠QPS = ∠RPS]
∵ Exterior ∠PSR = [∠PQS + ∠QPS]
and exterior ∠PSQ = [∠PRS + ∠RPS]
[An exterior angle is equal to the sum of interior opposite angles]
Now, from (1), we have
∠PSR = ∠PSQ.