CLASS-9 SUBJECT MATHS (FINALS-E) CHAPTER-7 (EXERCISE 7.4) TRIANGLES.

 EVENTS CONVENT HIGH SCHOOL

27/01/2022      CLASS- 9   SESSION 2021-22
SUBJECT : MATHS

CHAPTER-7 (EXERCISE7.4)
TRIANGLES

______________________________________

Question 1.Show that in a right angled triangle, the hypotenuse is the longest side.
Solution:
Let us consider ∆ABC such that ∠B = 90°
∴ ∠A + ∠B + ∠C = 180°
⇒ ∠A + 90°-+ ∠C = 180°
⇒ ∠A + ∠C = 90°
⇒∠A + ∠C = ∠B
∴ ∠B > ∠A and ∠B > ∠C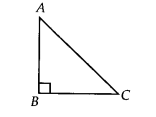

⇒ Side opposite to ∠B is longer than the side opposite to ∠A
i.e., AC > BC.
Similarly, AC > AB.
Therefore, we get AC is the longest side. But AC is the hypotenuse of the triangle. Thus, the hypotenuse is the longest side.

Question 2.In figure, sides AB and AC of ∆ABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.

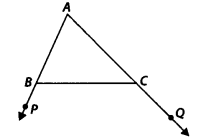
Solution:
∠ABC + ∠PBC = 180° [Linear pair]
and ∠ACB + ∠QCB = 180° [Linear pair]
But ∠PBC < ∠QCB [Given] ⇒ 180° – ∠PBC > 180° – ∠QCB
⇒ ∠ABC > ∠ACB
The side opposite to ∠ABC > the side opposite to ∠ACB
⇒ AC > AB.

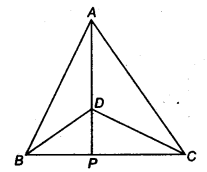
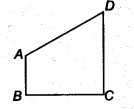
Question 3.In figure, ∠B <∠ A and ∠C <∠ D. Show that AD < BC.

Solution: Since ∠A > ∠B [Given]
∴ OB > OA …(1)
[Side opposite to greater angle is longer]
Similarly, OC > OD …(2)
Adding (1) and (2), we have
OB + OC > OA + OD
⇒ BC > AD

Question 4.AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see figure). Show that ∠ A > ∠C and ∠B >∠D.

Solution:
Let us join AC.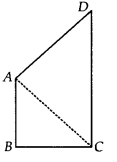

Now, in ∆ABC, AB < BC [∵ AB is the smallest side of the quadrilateral ABCD] ⇒ BC > AB
⇒ ∠BAC > ∠BCA …(1)
[Angle opposite to longer side of A is greater]
Again, in ∆ACD, CD > AD
[ CD is the longest side of the quadrilateral ABCD]
⇒ ∠CAD > ∠ACD …(2)
[Angle opposite to longer side of ∆ is greater]
Adding (1) and (2), we get
∠BAC + ∠CAD > ∠BCA + ∠ACD
⇒ ∠A > ∠C
Similarly, by joining BD, we have ∠B > ∠D.

Question 5.In figure, PR > PQ and PS bisect ∠QPR. Prove that ∠PSR >∠PSQ.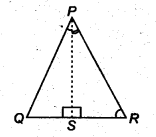

Solution:
In ∆PQR, PS bisects ∠QPR [Given]
∴ ∠QPS = ∠RPS
and PR > PQ [Given]
⇒ ∠PQS > ∠PRS [Angle opposite to longer side of A is greater]
⇒ ∠PQS + ∠QPS > ∠PRS + ∠RPS …(1) [∵∠QPS = ∠RPS]
∵ Exterior ∠PSR = [∠PQS + ∠QPS]
and exterior ∠PSQ = [∠PRS + ∠RPS]
[An exterior angle is equal to the sum of interior opposite angles]
Now, from (1), we have
∠PSR = ∠PSQ.

CLASS-9 SUBJECT MATHS (FINALS-E) CHAPTER-7 EXERCISE 7.3 TRIANGLES.

 EVENTS CONVENT H.SCHOOL

25/01/2022      CLASS- 9   SESSION 2021-22
SUBJECT :MATHS

CHAPTER-7 (EXERCISE 7.3)

TRIANGLES

______________________________________

Question 1.∆ABC and ∆DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to intersect BC at P, show that

(i) ∆ABD ≅ ∆ACD
(ii) ∆ABP ≅ ∆ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
Solution:
(i) In ∆ABD and ∆ACD, we have
AB = AC [Given]
AD = DA [Common]
BD = CD [Given]
∴ ∆ABD ≅ ∆ACD [By SSS congruency]
∠BAD = ∠CAD [By C.P.C.T.] …(1)

(ii) In ∆ABP and ∆ACP, we have
AB = AC [Given]
∠BAP = ∠CAP [From (1)]
∴ AP = PA [Common]
∴ ∆ABP ≅ ∆ACP [By SAS congruency]

(iii) Since, ∆ABP ≅ ∆ACP
⇒ ∠BAP = ∠CAP [By C.P.C.T.]
∴ AP is the bisector of ∠A.
Again, in ∆BDP and ∆CDP,
we have BD = CD [Given]
DP = PD [Common]
BP = CP [ ∵ ∆ABP ≅ ∆ACP]
⇒ A BDP = ACDP [By SSS congruency]
∴ ∠BDP = ∠CDP [By C.P.C.T.]
⇒ DP (or AP) is the bisector of ∠BDC
∴ AP is the bisector of ∠A as well as ∠D.

(iv) As, ∆ABP ≅ ∆ACP
⇒ ∠APS = ∠APC, BP = CP [By C.P.C.T.]
But ∠APB + ∠APC = 180° [Linear Pair]
∴ ∠APB = ∠APC = 90°
⇒ AP ⊥ BC, also BP = CP
Hence, AP is the perpendicular bisector of BC.

Question 2. AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that

(i) AD bisects BC
(ii) AD bisects ∠A
Solution:
(i) In right ∆ABD and ∆ACD, we have
AB =AC [Given]

∠ADB = ∠ADC [Each 90°]
AD = DA [Common]
∴ ∆ABD ≅ ∆ACD [By RHS congruency]
So, BD = CD [By C.P.C.T.]
⇒ D is the mid-point of BC or AD bisects BC.

(ii) Since, ∆ABD ≅ ∆ACD,
⇒ ∠BAD = ∠CAD [By C.P.C.T.]
So, AD bisects ∠A

Question 3.Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and OR and median PN of ∆PQR (see figure). Show that
(i) ∆ABC ≅ ∆PQR
(ii) ∆ABM ≅ ∆PQN

Solution:
In ∆ABC, AM is the median.
∴BM = 12 BC ……(1)
In ∆PQR, PN is the median.
∴ QN = 12QR …(2)
And BC = QR [Given]
⇒ 12BC = 12QR
⇒ BM = QN …(3) [From (1) and (2)]

(i) In ∆ABM and ∆PQN, we have
AB = PQ , [Given]
AM = PN [Given]
BM = QN [From (3)]
∴ ∆ABM ≅ ∆PQN [By SSS congruency]

(ii) Since ∆ABM ≅ ∆PQN
⇒ ∠B = ∠Q …(4) [By C.P.C.T.]
Now, in ∆ABC and ∆PQR, we have
∠B = ∠Q [From (4)]
AB = PQ [Given]
BC = QR [Given]
∴ ∆ABC ≅ ∆PQR [By SAS congruency]

Question 4.BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
Solution:
Since BE ⊥ AC [Given]

∴ BEC is a right triangle such that ∠BEC = 90°
Similarly, ∠CFB = 90°
Now, in right ∆BEC and ∆CFB, we have
BE = CF [Given]
BC = CB [Common hypotenuse]
∠BEC = ∠CFB [Each 90°]
∴ ∆BEC ≅ ∆CFB [By RHS congruency]
So, ∠BCE = ∠CBF [By C.P.C.T.]
or ∠BCA = ∠CBA
Now, in ∆ABC, ∠BCA = ∠CBA
⇒ AB = AC [Sides opposite to equal angles of a ∆ are equal]
∴ ABC is an isosceles triangle.